Lesson 2 Running you first classifier
Old models wont work as Fastai introduced a breaking change pin lib in diffrent env
fastai == 2.0.3
fastcore == 1.0.4
pytorch == 1.4.0
- Downloading data from Google Images: use the script go get all URLS run it in browser console
urls=Array.from(document.querySelectorAll('.rg_i')).map(el=> el.hasAttribute('data-src')?el.getAttribute('data-src'):el.getAttribute('data-iurl'));
window.open('data:text/csv;charset=utf-8,' + escape(urls.join('\n')));
- Creating validation set automatically from data
new API is DataBlock = template for creating a `DataLoaders````python
bears = DataBlock(
blocks=(ImageBlock, CategoryBlock),
get_items=get_image_files,
splitter=RandomSplitter(valid_pct=0.2, seed=42),
get_y=parent_label,
item_tfms=Resize(128))
dls = bears.dataloaders(path)
data = ImageDataBunch.from_folder(path, train=".", valid_pct=0.2,ds_tfms=get_transforms(), size=224, num_workers=4).normalize(imagenet_stats)

np.random.seed(42) is always set to same number here so that validation set remains same and improve our model independant of data changes.
We also use RandomResizedCrop to use a n random crop in every epoch
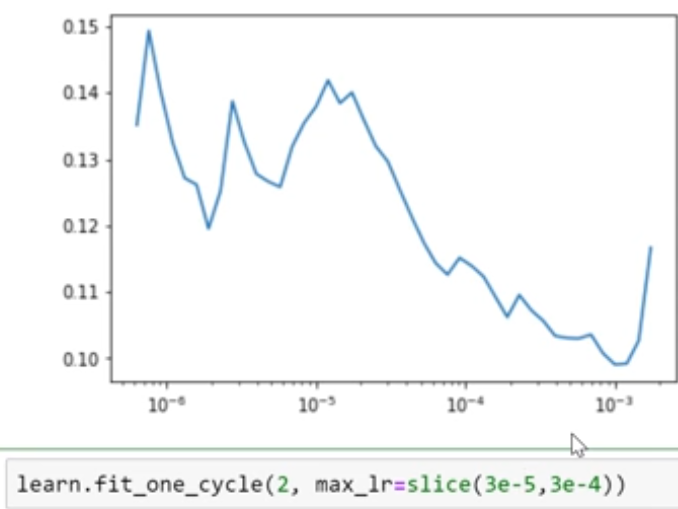
- Tips for choosing learning rate: Look for the range where the accuracy is imroving steadily (not very steep).
ex here the error rate decrese is steady between &10^-5& and &10^-4& so we use
learn.fit_one_cycle(2, max_lr=slice(3e-5,3e-4))
![learn_rate]
- All data sets have x and y
x = file name
y = labels - You can create application with UI inside Jupyter notebooks.
open_image(path)fn to open any imagelearn.export()exports the trained model to export.pkl its ~99MB- Starlette is web app toolkit similar to flas which has async/await style
- Trainining loss > validation loss means data is not properly fitted
- Too many epochs leads to overfitting. It happens when error rate seems to be going down tthen in subsequents epochs start going up.
Lesson 2: SGD
Stochastic Gradient Descent (SGD)
Tensor in deeplearning it is nothing but a array ( 1 or more dimensions) which is of regular shape (all rows are of equal size)
Rank: number of dimensions
x = matrix/ vector = tensor
a = matrix/ vector = tensor
y = x@a = matrix product
Mean squared Error MSE is the common error fn for regression
def mse(y_hat, y): return ((y_hat-y)**2).mean()
y_hat or $\hat{y}$ is predicted value and y is the actual
tensor(-1.,1) is eqivalent to tensor(-1.0,1.0) we do this because we want everything to be float
In this we are trying to fit a line of the form
y = mx +c which we convert to
$y_i$ = $a_1x_{1i} + a_2x_{2i}$ where $x_2$ = 1
We first try to gues $a_1,a_2$ and calculate MSE. we then try minimise MSE
We can do that either try to keep guessing by changing $a_1,a_2$ up and down and calculate MSE and see where it reduces or we can use Maths in which a derivative calculates the same thing
Gradient/Derivative~ tells us whether moving it up or down $a_2$ or tilting it up or down $a_1$ make it better i.e change the MSE.
Gradient descent is an algorithm that minimizes functions. Given a function defined by a set of parameters, gradient descent starts with an initial set of parameter values and iteratively moves toward a set of parameter values that minimize the function. This iterative minimization is achieved by taking steps in the negative direction of the function gradient.
mini-batches
In this ex we calculated loss for all the points in practice it willnot possible as tehre will be too mnay points when the rank/complexity increases.
So we use Mini batches for every epoch/iteration we calculate loss from a random subset of points
Model or Architecture is nothing but the mathematical fn here it is y = mx + c or $y = a_1x_1 + a_2x_2$
Parameter are the coefficients or weights are the number which we are trying to find here they are $a_1 and\ a_2$
How (and why) to create a good validation set? link